Difference between revisions of "Spell Success"
m (→Step down) |
m (→Step down) |
||
| Line 79: | Line 79: | ||
|Very Good||-24||20% | |Very Good||-24||20% | ||
|- | |- | ||
| − | |Great||-80 | + | |Great||-80||10% |
|- | |- | ||
|Excellent||-140||4% | |Excellent||-140||4% | ||
|- | |- | ||
| − | |Perfect||-180 | + | |Perfect||-180||0% |
|- | |- | ||
|} | |} | ||
Revision as of 00:41, 16 May 2023
Spell success is the rate at which casting a spell can be expected to succeed. Spell success rate is determined by a complex combination of:
- Spell level
- Spell-related skills, Intelligence
- Penalties from body armour and shields (mitigated by Armour skill / Shields skill)
- Modifiers like Wizardry and Wild Magic
Base Chance
The source code talks in terms of chance of failure, not success. Therefore, we want the spellFailure chance to be as low as possible - in fact, to reach a 0% success rate, your chance to fail has to be negative. More on that below.
The base failure before any modifiers is as follows:
spellFailure = 60
- [6 * spell skills]
- [2 * Intelligence]
+ Spell difficulty
+ Armour/shield penalty
- 60 is an arbitrary base chance of failure.
- Increasing intelligence and spell skills (spells of that skill and Spellcasting) will decrease failure.
- Higher level spells are more difficult, wearing armour/shields make it more difficult.
spellFailure, at this stage, is capped at 1400.
Skill
"Spell skills" is the combination of Spellcasting and an average of a spells schools (e.g. a Conjurations / Fire spell will take the average of the Conjurations skill and Fire Magic skill). This is calculated with the following two equations:
Z = [Spellcasting / 2] + [Average(SpellSkills) * 2]
spell skills = 50 * log_2 (1 + Z / 50)
With 27 in Spellcasting and 27 in relevant skills, the total value of (6 * spell skills) is capped at 370.
Spell level
Higher level spells are more difficult. Each level of spell adds a number to your spell failure rate.
spellDifficulty = 3 (level 1)
15 (level 2) (+12)
35 (level 3) (+20)
70 (level 4) (+35)
100 (level 5) (+30)
150 (level 6) (+50)
200 (level 7) (+50)
260 (level 8) (+60)
330 (level 9) (+70)
Armour and shield penalties
(Under Construction)
Armour/Shield Penalty = 19 * (armour penalty) + 19 * (shield penalty)
armour penalty = 0.4 * (Encumbrance Rating)^2
* (45 - Armour skill Lv) / 45
/ (Str + 3)
shield penalty = max(0, (EV Penalty) - (Shield Skill Lv) / (Player species factor) )
Player species factor is 5 for normal species, 3 for large species, and 7 for small species, respectively. Spriggans have 9, though they only can use bucklers.
Step down
At this point, the spell failure is put through a stepdown curve. If it's over 45, it's unaffected, otherwise it needs to be progressively lower to improve the overall result. This is a stepwise curve, and complex to describe. In the table is the listed native chance to reach certain points (i.e., spell success bands). This is not the final spell rate; there are more modifiers.
| Description | spellFailure | Raw Failure Rate |
|---|---|---|
| Fair | 45 | 45% |
| Good | 10 | 30% |
| Very Good | -24 | 20% |
| Great | -80 | 10% |
| Excellent | -140 | 4% |
| Perfect | -180 | 0% |
From −60 to −180, this equation is linear; each difference of 20 gives 2% to the final spell success chance. Penalties are more meaningful the higher your spell failure chance is.
Modifiers
The following modifiers are added after the STEPPED DOWN failure rates. However, they are still raw success chance, and are adjusted by a sigmoid function later.
Positive (+spell failure):
Wild Magic: +4% per level Orb of energy: +10% Crystal ball of Wucad Mu: +20% Vertigo: +7%
Negative (-spell failure):
Subdued Magic: -2% per level Wizardry: -25% for 1 source, -33% for 2, -50% for 3
Vehumet gives 2 levels of wizardry for destructive spells.
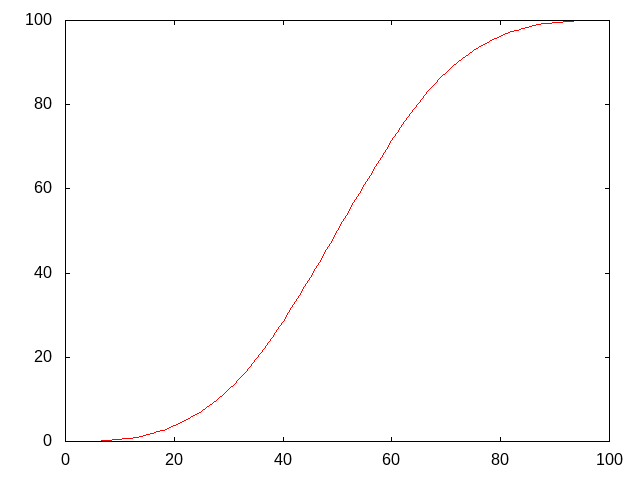
After all modifiers have applied, you will get a cumulative raw spell success chance. This is converted into the final success via the function below.
Final Step
The number we have obtained isn't the final chance of failure. The game doesn't compare that number with a random number between 0 and 99, but with the sum of three numbers divided by three.
(1d101 + 1d101 + 1d100 - 3)/3 < fail chance
This is equivalent to applying this transformation to the chance of failure:
This sigmoid function makes it more difficult to decrease your failure rate when it is high or low, but it will go down very quickly when it is in the middle. Up to raw failure rate of 33%, one can use this formula:
N = (raw_failure_rate) * 3 Real Failure Rate = N * (N+1) * (N+2) / 6 / 101 / 101 (in unit of %)
This can be tabulated for usefulness.
| Raw Fail chance | Actual fail chance |
|---|---|
| 32% | 14.9% |
| 30% | 12.3% |
| 28% | 10.0% |
| 26% | 8.1% |
| 24% | 6.4% |
| 22% | 4.9% |
| 20% | 3.7% |
| 18% | 2.7% |
| 16% | 1.9% |
| 14% | 1.3% |
| 12% | 0.8% |
Strategy
It is debatable whether the following formulae are of real use during a game. However, inflection points such when the extra armour EV penalty disappears are fairly easy to discern. Calculating this stuff on the fly is only for savants! However, one can refer example section of this page for Lv 9 magics, which requires tremendous amount of experience to be stabilized.
Example: Fire Storm
For the failure rate of 10%, a raw failure rate of 28% is required. Let's set Int=32, a decent value for spellcasters but not sufficient for end-game annihilator. Assuming no armour/shield penalty. This argument can be applied with any of Lv 9 spells, if one exclude Vehumet effect.
- Without any aid: Raw rate of 2% is stepped down to 28%, so 2% is the point that should be achieved. This is equivalent to 54.0 point of spell skills, requiring (school skill*2 + spellcasting*0.5) = 55.7. Even if the spellcasting is maxed out to 27, the average school skill value of 21.1 is required to cast Fire storm within 10% failure.
- With an aid of a wizardry ring: A wizardry option knocks 1/4 of failure rate before sigmoid function, so the required raw fail rate is 38%. Raw rate of 32% is stepped down to 38%, and (school skill*2 + spellcasting*0.5) = 48.6. This value is quite easy to be achieved now, and average of 19.4 Lv including spellcasting is sufficient for 10% failure rate.
- Vehumet worshipper, or two wizardry rings: These enhancements knock off 1/3 of failure rate before sigmoid. Now the raw fail rate required before stepdown is 38%, and (school skill*2 + spellcasting*0.5) = 47.3. Required average skill Lvs, including spellcasting, is 18.9. Worshipping Vehumet really offers tremendous benefits for high-level spells.
- Vehumet with a wizardry ring: Maxed out enhancer effect. Raw fail rate of 56% can be used without stepdown, and (school skill*2 + spellcasting*0.5) = 43.3. Required average skill Lvs, including spellcasting, is 17.3. If one regulates spellcasting up to 15, then 17.9 Lv of each school level is sufficient!