Difference between revisions of "Spell Success"
m (the example used the old formula; add a rough note) |
m (→Strategy) |
||
| Line 164: | Line 164: | ||
== Strategy == | == Strategy == | ||
| − | It is debatable whether these formulae are of any | + | It is debatable whether these formulae are of any practical use. |
However, high level spells take a massive amount of XP to train, and it can be useful to know how many levels you need, or know the armour you can afford to wear in order to cast a specific spell (in the long term). | However, high level spells take a massive amount of XP to train, and it can be useful to know how many levels you need, or know the armour you can afford to wear in order to cast a specific spell (in the long term). | ||
| + | |||
| + | <!-- This example is currently outdated, but the numbers should be roughly similar | ||
===Example: [[Fire Storm]]=== | ===Example: [[Fire Storm]]=== | ||
| − | |||
For an actual failure rate of 10%, a raw failure rate of 28% is required. Assume Int=32, a good value for a dedicated caster (if a bit low). Also assume no armour/shield penalty. | For an actual failure rate of 10%, a raw failure rate of 28% is required. Assume Int=32, a good value for a dedicated caster (if a bit low). Also assume no armour/shield penalty. | ||
| Line 181: | Line 182: | ||
* '''Vehumet + Wizardry / Wizardry x3''': Maxed out enhancer effect. Raw fail rate of 56% can be used without stepdown, and <code>(school skill*2 + spellcasting*0.5) = 43.3</code>. Required average skill Lvs (including spellcasting) is 17.3. If one regulates spellcasting up to 15, then 17.9 Lv of each school level is sufficient! | * '''Vehumet + Wizardry / Wizardry x3''': Maxed out enhancer effect. Raw fail rate of 56% can be used without stepdown, and <code>(school skill*2 + spellcasting*0.5) = 43.3</code>. Required average skill Lvs (including spellcasting) is 17.3. If one regulates spellcasting up to 15, then 17.9 Lv of each school level is sufficient! | ||
| − | These numbers can be applied to any level 9 spell. | + | These numbers can be applied to any level 9 spell. --> |
==See also== | ==See also== | ||
Revision as of 07:38, 22 May 2023
Spell success is the rate at which casting a spell can be expected to succeed. Spell success rate is determined by a complex combination of:
- Spell level
- Spell-related skills, Intelligence
- Penalties from body armour and shields (mitigated by Armour skill / Shields skill)
- Modifiers like Wizardry and Wild Magic
Base Chance
The source code talks in terms of chance of failure, not success. Therefore, we want the spellFailure chance to be as low as possible - in fact, to reach a 0% success rate, your chance to fail has to be negative. More on that below.
The base failure before any modifiers is as follows:[1]
spellFailure = 60
- [6 * spell_skills]
- [2 * Intelligence]
+ Spell difficulty
+ Encumbrance penalties
- 60 is an arbitrary base chance of failure.
- Increasing intelligence and spell skills (skills respective to the spell and Spellcasting) will decrease failure.
- Higher level spells are more difficult, wearing armour/shields make it more difficult.
spellFailure, at this stage, is capped at 1400.
Spell skills
"Spell_skills" takes into account Spellcasting and an average of a spell's schools (e.g. a Conjurations / Fire spell will take the average of the Conjurations skill and Fire Magic skill). This is calculated with the following equation:[2] [3]
spell_skills = [Spellcasting / 2] + [Average(Skill_level) * 2]
For Djinn, the Spellcasting skill is counted as both Average Spell Schools and Spellcasting itself, resulting in the following formula:[4]
spell_skills = Spellcasting * 2.5
With 27 in Spellcasting and 27 in relevant skills, the total value of (6 * spell_skills) is capped at 405.
Spell difficulty
Higher level spells are more difficult. Each level of spell adds a number to your spell failure rate:[5]
spellDifficulty = 3 (level 1)
15 (level 2) (+12)
35 (level 3) (+20)
70 (level 4) (+35)
100 (level 5) (+30)
150 (level 6) (+50)
200 (level 7) (+50)
260 (level 8) (+60)
340 (level 9) (+80)
Encumbrance penalties
Both Armour and Shield penalties for spells are derived from their EV penalties. First, calculate the ev penalty, then calculate the spell penalty. Armour and Shields do not influence each other.
Armour
ev penalty = 2 * encumbrance^2 * (450 - 10 * armour_skill) / 5 (str +3) spell penalty = 19 * ev penalty
Shield
ev penalty = 2/5 * encumbrance^2 / (5 + str) * (27 - shield_skill) / 27 spell penalty = 19 * (ev penalty - (shield_skill) / (size factor + 5))
Size factor is determined by species:
| Size | Races | Size factor | Size factor +5 |
|---|---|---|---|
| Little | Spriggan | +4 | 9 |
| Small | Kobold | +2 | 7 |
| Normal | most species | 0 | 5 |
| Normal (strong arms) |
Formicid | -2 | 3 |
| Large (normal torso) |
Armataur, Naga | -2 | 3 |
| Large | Ogre, Troll | -2 | 3 |
Step down
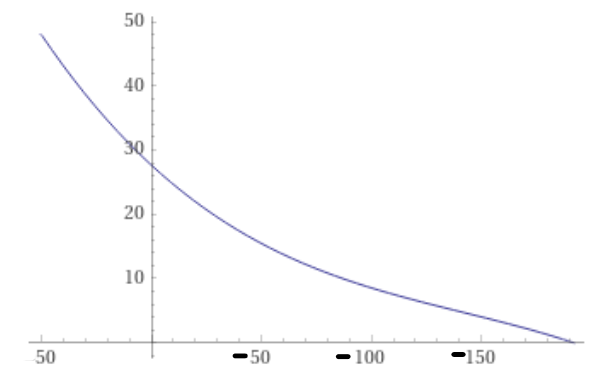
At this point, the spell failure is put through a complicated post-processing curve:[6]
(x^3 + 426x^2 + 82670x + 6983254) / 262144 IF spellFailure < 43
This replicates a step-down curve:
This curve has the following points:
- spellFailure >= 43 is unmodified, so a spellFailure of 43 would equate to a Raw Failure Rate of 43%.
- spellFailure = -72 reaches a Raw Failure Rate of 10%.
- spellFailure = -173 reaches a Raw Failure Rate of 0%.
This is not the final spell rate; there are more modifiers.
Modifiers
The following modifiers are added after the STEPPED DOWN failure rates. However, they are still raw spell failure chance, and are adjusted by a sigmoid function later. [7]
Positive (+spell failure):
- Wild Magic: +4% per level
- Disrupted Magic (-Wiz) sacrifice: +4% per level
- Orb of energy: +10%
- Crystal ball of Wucad Mu: +20%
- Vertigo: +7%
Negative (-spell failure):
- Subdued Magic: -2% per level
- Wizardry: x75% for 1 source, x66.6% for 2, x50% for 3 (applied after all other factors)
Vehumet gives 2 levels of wizardry for destructive spells.
After all modifiers have applied, you will get a cumulative raw spell failure chance. This is converted into the final success via the function below.
Final Step
The number we have obtained isn't the final chance of failure. The game doesn't compare that number with a random number between 0 and 99, but with the sum of three numbers divided by three.[8]
(1d101 + 1d101 + 1d100 - 3)/3 < fail chance
This is equivalent to applying this transformation to the chance of failure:
This sigmoid function makes it more difficult to decrease your failure rate when it is high or low, but it will go down very quickly when it is in the middle. For raw failures below 33%, one can use this formula:
N = (raw_failure_rate) * 3 Real Failure Rate = N * (N+1) * (N+2) / 6 / 101 / 101 (in unit of %)
This can be tabulated for usefulness.
| Raw Fail chance | Actual fail chance |
|---|---|
| 32% | 14.9% |
| 30% | 12.3% |
| 28% | 10.0% |
| 26% | 8.1% |
| 24% | 6.4% |
| 22% | 4.9% |
| 20% | 3.7% |
| 18% | 2.7% |
| 16% | 1.9% |
| 14% | 1.3% |
| 12% | 0.8% |
Strategy
It is debatable whether these formulae are of any practical use.
However, high level spells take a massive amount of XP to train, and it can be useful to know how many levels you need, or know the armour you can afford to wear in order to cast a specific spell (in the long term).
See also
History
- Prior to 0.22, spell_schools went through a stepdown,
50 * log2(1 + spell_schools)/50), which penalized the caster if(Spellcasting/2) + (2* AvgSpellSchool) > 50. However, spellFailure for level 9 spells was 330 instead of 340. - Prior to 0.20, the Step down function was different, relying on breakpoints rather than a polynomial. Also, more breakpoints existed elsewhere in the spell failure calculation.
References
- ↑ spl-cast.cc:406 (0.30.0)
- ↑ spl-cast.cc:413 (0.30.0)
- ↑ spl-cast.cc:377 (0.30.0)
- ↑ spl-cast.cc:391 (0.30.0)
- ↑ spl-cast.cc:422 (0.30.0)
- ↑ spl-cast.cc:463 (0.30.0)
- ↑ spl-cast.cc:466 (0.30.0)
- ↑ spl-cast.cc:2533 (0.30.0)