Spell Success

Version 0.30: This article may not be up to date for the latest stable release of Crawl.

Spell success is the rate at which casting a spell can be expected to succeed. Spell success rate is determined by a complex combination of:

1. Spell level
2. Spell-related skills, Intelligence
3. Penalties from body armour and shields (mitigated by Armour skill / Shields skill)
4. Modifiers like Wizardry and Wild Magic

Base Chance

The source code talks in terms of chance of failure, not success. Therefore, we want the spellFailure chance to be as low as possible - in fact, to reach a 0% success rate, your chance to fail has to be negative. More on that below.

The base failure before any modifiers is as follows:

 spellFailure = 60
              - [6 * spell_skills]
              - [2 * Intelligence]
              + Spell difficulty
              + Encumbrance penalties

• 60 is an arbitrary base chance of failure.
• Increasing intelligence and spell skills (skills respective to the spell and Spellcasting) will decrease failure.
• Higher level spells are more difficult, wearing armour/shields make it more difficult.

spellFailure, at this stage, is capped at 1400.

Spell skills

"Spell_skills" takes into account Spellcasting and an average of a spell's schools (e.g. a Conjurations / Fire spell will take the average of the Conjurations skill and Fire Magic skill). This is calculated with the following equation:

 spell_skills = [Spellcasting / 2] + [Average(Skill_level) * 2]

For Djinn, the Spellcasting skill is counted as both Average Spell Schools and Spellcasting itself, resulting in the following formula:

 spell_skills = Spellcasting * 2.5

With 27 in Spellcasting and 27 in relevant skills, the total value of (6 * spell_skills) is capped at 405.

Spell difficulty

Higher level spells are more difficult. Each level of spell adds a number to your spell failure rate:

 spellDifficulty =   3 (level 1)
                    15 (level 2)   (+12)
                    35 (level 3)   (+20)
                    70 (level 4)   (+35)
                   100 (level 5)   (+30)
                   150 (level 6)   (+50)
                   200 (level 7)   (+50)
                   260 (level 8)   (+60)
                   340 (level 9)   (+80)

Encumbrance penalties

Both Armour and Shield penalties for spells are derived from their EV penalties. First, calculate the ev penalty, then calculate the spell penalty. Armour and Shields do not influence each other.

Armour

 ev penalty = 1/225 * encumbrance^2 * (90 - 2 * armour_skill) / (str +3)
 spell penalty = 19 * ev penalty

Shield

 ev penalty = 2/5 * encumbrance^2 / (5 + str) * (27 - shield_skill) / 27
 spell penalty = 19 * (ev penalty - (shield_skill) / (size factor + 5))

Size factor is determined by species:

Size	Races	Size factor	Size factor +5
Little	Spriggan	+4	9
Small	Kobold	+2	7
Normal	most species	0	5
Normal (strong arms)	Formicid	-2	3
Large (normal torso)	Armataur, Naga	-2	3
Large	Ogre, Troll	-2	3

Step down

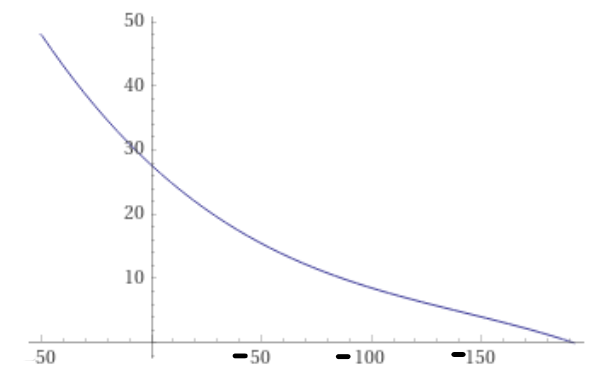
At this point, the spell failure is put through a complicated post-processing curve:

(x^3 + 426x^2 + 82670x + 6983254) / 262144 IF spellFailure < 43

This replicates a step-down curve:

x-axis = spellFailure, y-axis = Raw Failure Rate

This curve has the following points:

SpellFailure	Raw Fail chance
43	43%
25	36.6%
0	27.7%
-50	15.5%
-72	10%
-100	8.5%
-173	0%

This is not the final spell rate; there are more modifiers.

Modifiers

The following modifiers are added after the STEPPED DOWN failure rates. However, they are still raw spell failure chance, and are adjusted by a sigmoid function later.

Positive (+spell failure):

• Wild Magic: +4% per level
• Disrupted Magic (-Wiz) sacrifice: +4% per level
• Orb of energy: +10%
• Crystal ball of Wucad Mu: +20%
• Vertigo: +7%

Negative (-spell failure):

• Subdued Magic: -2% per level
• Wizardry: x75% for 1 source, x66.6% for 2, x50% for 3 (applied after all other factors)

Vehumet gives 2 levels of wizardry for destructive spells.

After all modifiers have applied, you will get a cumulative raw spell failure chance. This is converted into the final success via the function below.

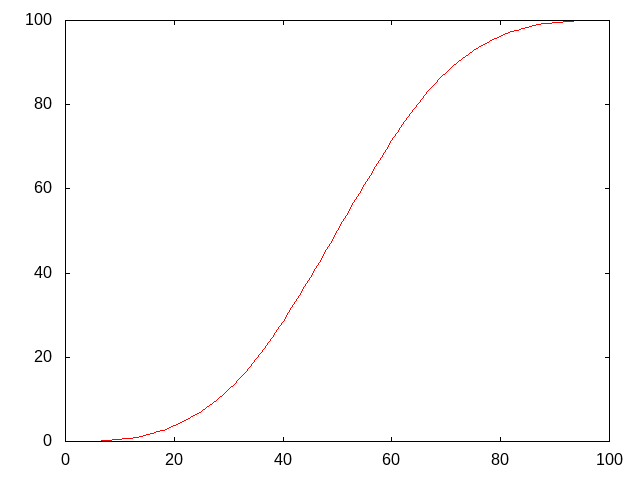
Final Step

In short, the game doesn't compare your raw failure chance with a number from 0 to 99. Instead, it compares the raw failure to the sum of three numbers divided by three.

(1d101 + 1d101 + 1d100 - 3)/3 < fail chance

This is equivalent to applying this transformation to the chance of failure:

This sigmoid function makes it more difficult to decrease your failure rate when it is high or low, but it will go down very quickly when it is in the middle. For raw failures below 33%, one can use this formula:

 N                 = (raw_failure_rate) * 3
 Real Failure Rate = N * (N+1) * (N+2) / 6 / 101 / 101 (in unit of %)

This can be tabulated for usefulness.

SpellFailure	Raw Fail chance	Actual fail chance
13	32%	14.9%
7	30%	12.3%
1	28%	10.0%
-6	26%	8.1%
-12	24%	6.4%
-20	22%	4.9%
-28	20%	3.7%
-37	18%	2.7%
-47	16%	1.9%
-58	14%	1.3%
-71	12%	0.8%

Strategy

It is debatable whether these formulae are of any practical use during a game.

It may be nice to know a few things from a strategic point of view.

• High level spells take a massive amount of XP to train, and it can be useful to know how many levels you'd need.
• You can quantize your level of armour encumbrance. For example, a caster could say "a set of fire dragon scales gives a spell penalty equal to 9 levels of a spell school". Then, you could determine if wearing FDS is worth it, both short-term ("can I cast a spell in this right now?") and long-term ("can I cast a spell in this when I reach Zot?").
• You can calculate the relative value of a skill. For example, you can see when a level of <Spell School> would be more valuable than a level of Armour skill, or when a point of strength is worth more than a point of intelligence.

Of course, this isn't necessary. You can derive most (if not all) of this information by just checking your spell failure. If you wear a pierce of armour, and determine that your spell failure is unacceptable, then don't wear that armour - no need to calculate it! After you trained your skill a bit, you can wear a desired armour again, and see if it's any better.

See also

• Spell power
• Miscast effect

History

• Prior to 0.22, spell_schools went through a stepdown, 50 * log2(1 + spell_schools/50), which penalized the caster if (Spellcasting/2) + (2* AvgSpellSchool) > 50. However, spellFailure for level 9 spells was 330 instead of 340.
• Prior to 0.20, the Step down function was different, relying on breakpoints rather than a polynomial. Also, more breakpoints existed elsewhere in the spell failure calculation.